Tolérance

Le paramètre Tolérance apparaît dans de nombreux Transformers qui effectuent des tâches de relations spatiales telles que l'intersection, la superposition et la dissolution.

La tolérance est une distance en unités terrestres. Les points situés à cette distance les uns des autres peuvent être ajustés exactement au même endroit.

Cette valeur est souvent très, très faible, mais elle est suffisante pour éviter les artefacts et améliorer les résultats. Elle n'est jamais nulle.

En général, il est recommandé d'utiliser le paramètre Automatique.

Pourquoi avons-nous besoin de la tolérance ?

Il existe de multiples raisons d'inclure la tolérance dans l'analyse spatiale :

• Les points représentant la même position dans le monde réel peuvent avoir des coordonnées légèrement différentes en raison des méthodes de mesure, du niveau de précision et de l'erreur.
• Les calculs spatiaux peuvent produire des coordonnées avec une précision bien supérieure à ce qui est utile.
• Les calculs sont effectués avec une arithmétique de 64 bits, ce qui peut introduire et accumuler des erreurs.
• Les nombres sont souvent arrondis pour respecter les exigences en matière de taille de stockage. Cette erreur d'arrondi peut se propager dans les calculs ultérieurs et entraîner un désalignement et des écarts entre les géométries.

Les écarts sont minimes, mais doivent être pris en compte.

Emplacement et intersections

Les coordonnées existent sur une grille. Dans la plupart des cas, l'intersection de deux lignes se situera quelque part entre les points de la grille, avec des valeurs de coordonnées calculées dont la précision (décimales) dépasse largement ce qui est précis et utile dans l'espace de coordonnées.

Si ces résultats sont utilisés pour d'autres calculs, de minuscules différences s'accumulent et font boule de neige, produisant des fragments de géométrie indésirables (et dépourvus de sens).

La tolérance permet d'éviter cela, en reliant les points entre eux lorsque c'est nécessaire.

Stockage binaire, mathématiques et arrondis

Les différences entre les coordonnées au même endroit peuvent être introduites par la nature du calcul et du stockage des nombres.

Stockage des décimales en binaire 64 bits

Considérons le résultat de la division de dix par trois ( 10/3 ). Le résultat est 3.3333333333... Le nombre 3 se répète à l'infini et est généralement arrondi à une précision utile (nombre de décimales).

De même, certains calculs finissent par se répéter en binaire.

Un divisé par cinq ( 1/5 ) en décimal est :

0.2

Le résultat en binaire est cependant :

0.0111 1111 1001 0011 0011 0011 0011 0011…

Le 0011 se répète à l'infini, tout comme le 10/3 en décimal. L'ordinateur l'arrondit à la valeur mathématique la plus proche, soit 0x3FC999999999999A en hexadécimal ou en décimal :

0.200000000000000011102230246252

La différence est infime, mais nécessite l'application d'une tolérance.

Quelle valeur de tolérance faut-il utiliser ?

Si l'option Automatique est disponible, elle doit généralement être utilisée. La valeur réelle est écrite dans le fichier journal.

Dans ce fichier journal, un dissolveur traite plusieurs groupes d'entités dans un système de coordonnées UTM (unités terrestres en mètres) et calcule la valeur de tolérance optimale pour chaque groupe.

Notez que les valeurs sont extrêmement faibles et que chacune d'entre elles est très légèrement différente.

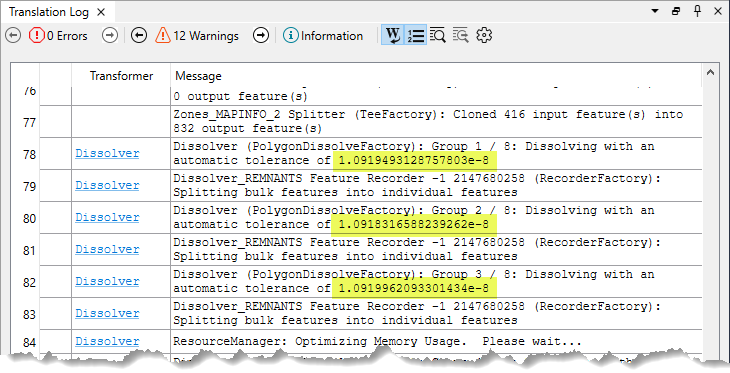
Des valeurs explicites peuvent être saisies pour annuler ce comportement, mais elles doivent être supérieures à zéro et à la valeur de tolérance automatique.

Comment la tolérance est-elle utilisée ?

La tolérance est appliquée à l'aide d'un ajustement de sommet ancré.

Les entités sont ancrées autour des points existants. Les données sont déplacées le moins possible et les entités sont plus susceptibles d'être connectées à des endroits topologiquement significatifs.