Arcs (IFMEArc)
Il y a 3 façons de représenter un arc dans FME.
ArcByCenterPoint
Les entités arc de ce type possèdent une coordonnée x/y qui représente leur point central, ainsi qu'une définition mathématique du rayon de l'arc et des angles de balayage. Les arcs peuvent être elliptiques, en ce sens qu'ils peuvent avoir des valeurs de rayon primaire et secondaire différentes. Ils peuvent également avoir une rotation. La définition de l'arc implique des emplacements de début et de fin, mais parfois ces emplacements peuvent aussi être définis explicitement.
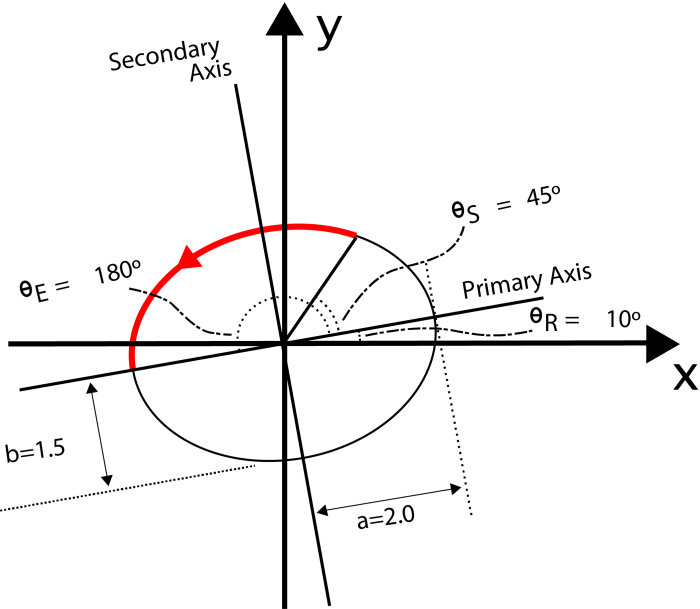
L’équation cartésienne de l'ellipse définit la courbe par une forme paramétrique simple, avec des échelles différentes pour les coordonnées x et y.
x = a cos(t)
y = b sin(t)
où
a = axe primaire
b = axe secondaire
Notez que t est un paramètre qui n'a pas d'interprétation directe en termes d'angle. Cependant, la relation entre l'angle polaire (thêta) à partir du centre de l'ellipse et le paramètre t découle de :
theta = arctan((b/a)*tan(t))
ou
t = arctan((a/b)*tan(theta))
Exemple: Pour spécifier, dans le diagramme ci-dessus, l'arc rouge dans l'ordre inverse des aiguilles d'une montre, les valeurs suivantes doivent être précisées sur l'entité :
Grand rayon = a = 2.0
Petit rayon = b = 1.5
Rotation = thetaR = 10 (degrés)
Angle de démarrage = tS = arctan((a/b)*tan(thetaS)) = arctan((2.0/1.5)*tan(45)) = 53.130102354155978703144387440907
Angle de balayage = tE - tS = arctan((a/b)*tan(thetaE)) - tS = arctan((2.0/1.5)*tan(180)) - tS = 180.0 - tS = 180.0 - 53.130102354155978703144387440907 = 126.86989764584402129685561255909
Optionnellement, l'arc peut avoir des points finaux spécifiques.
Si l'arc est en 3D ou a des mesures, l'emplacement du z et les valeurs de mesures sont définis comme tel :
- Si l'arc a des points d'extrémité explicites, le point central est en 2D sans mesures et les points d'extrémité peuvent avoir des valeurs de z et/ou de mesures uniques. Les points d'extrémité doivent tous deux être en 2D ou en 3D et doivent avoir le même nombre et le même nom de mesures, mais les valeurs de ces dernières entre eux peuvent différer.
- Si l'arc n'a pas de points finaux explicites, le point central peut avoir une valeur z unique et/ou des valeurs de mesure applicables à l'arc dans son ensemble.
ArcByBulge (Arc par bosse)
Une autre définition d'arc est une valeur de renflement, plus les deux coordonnées uniques du point d'extrémité. Cette définition ne peut représenter que des arcs circulaires, non fermés.
La valeur de "bosse" doit être comprise en -1.0 et 1.0 et détermine le niveau de courbe entre ces deux points.

Si l'arc a des valeurs z ou des mesures, les points d'extrémité peuvent avoir des valeurs z et/ou des mesures uniques. Les extrémités doivent être toutes deux en 2D ou en 3D, et doivent avoir le même nombre et les mêmes mesures, mais les valeurs de ces dernières entre elles peuvent différer.
ArcBy3Points
Une autre définition de l'arc est constituée des deux points d'extrémité, plus le point central de la "ligne" de l'arc. (Le point médian ne doit pas nécessairement se trouver exactement à mi-chemin, mais au moins quelque part le long de l'arc). Les trois points doivent être uniques. Cette définition ne peut représenter que des arcs circulaires et non fermés.
Si l'arc a des valeurs z ou des mesures, les trois points peuvent avoir des valeurs z et/ou des mesures uniques. Les points doivent tous être en 2D ou en 3D, et doivent avoir le même nombre et le même nom de mesures, mais les valeurs de ces dernières entre eux peuvent différer.
Voir aussi