3DAffiner

Effectue une transformation affine 3D (comme le décalage, la rotation ou l'échelle) sur les coordonnées de l'entité.

Cas d'utilisation courants

Déplacement, mise à l'échelle et rotation de la géométrie 3D.

Comment fonctionne-t-il ?

Le 3DAffiner reçoit des entités de n'importe quel type de géométrie et déplace leurs coordonnées x, y et z selon une transformation affine spécifiée.

Une transformation affine 3D est une méthode mathématique de modification de la géométrie qui :

Préserve les lignes et colinéarité : tous les points sur une ligne droite ou un plan sont toujours sur une ligne droite ou un plan après la transformation.
Préserve le parallélisme : les lignes et les plans qui sont initialement parallèles le sont toujours après transformation.
Peut ne pas préserver les angles, les longueurs ou les surfaces, selon le type de transformation effectuée.

La mise à l'échelle, la mise en miroir, la rotation, le cisaillement et la translation (relocalisation ou décalage) sont tous des traitements affines. Elles peuvent être effectuées séparément ou en combinaison.

3DAffiner effectue des transformations 3D, en utilisant cette formule :

x' = Ax + By + Cz + D

y' = Ex + Fy + Gz + H

z' = Ix + Jy + Kz + L

Où (x,y,z) sont les coordonnées d'entrée et (x',y',z') sont les coordonnées de sortie transformées.

	Description	Formule/Coefficients	Exemples
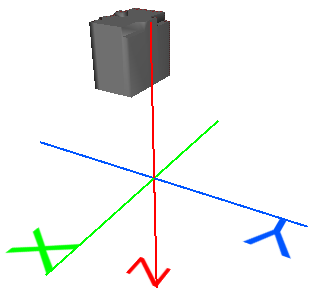
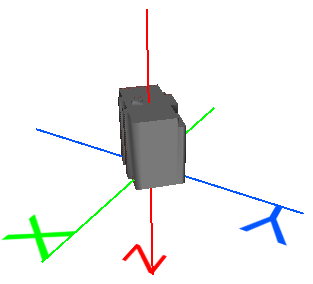
Objet 3D original	Ce modèle de bâtiment 3D est centré à l'origine (0,0,0) et ses unités sont les mètres. Il n'est pas géoréférencé.
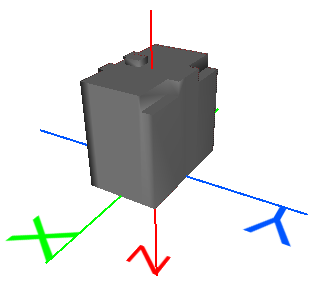
Translation	Déplacer la géométrie d'une distance fixée.	x' = 1x + 0y + 0z + D y' = 0x + 1y + 0z + H z' = 0x + 0y + 1z + L Simplifié : x' = x + D y' = y + H z' = z + L D = X offset H = Y offset L = Z offset	Déplacer un objet de 22 mètre le long de tous les axes : x' = 1x + 0y + 0z + 22 y' = 0x + 1y + 0z + 22 z' = 0x + 0y + 1z + 22
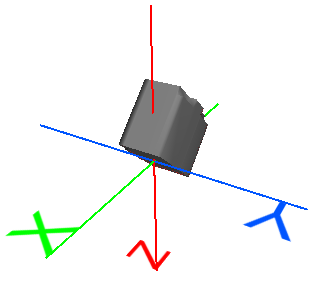
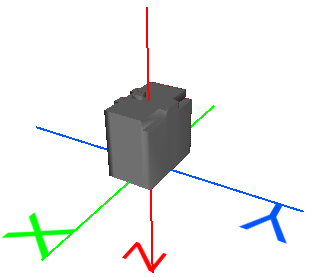
Échelle	Rétrécit ou agrandit la géométrie.	x' = Ax + 0y + 0z + 0 y' = 0x + Fy + 0z + 0 z' = 0x + 0y + Kz + 0 Simplifié : x' = Ax y' = Fy z' = Kz A = facteur d'échelle X F = facteur d'échelle Y K = facteur d'échelle Z	Agrandit l'objet par un facteur d'échelle de 1,5 : x' = 1.5x + 0y + 0z + 0 y' = 0x + 1.5y + 0z + 0 z' = 0x + 0y + 1.5z + 0
Pivote selon X	Pivote la géométrie autour de l'axe X.	x' = 1x + 0y + 0z + 0 y' = 0x + cos(ϴ)y + −sin(ϴ)z + 0 z' = 0x + sin(ϴ)y + cos(ϴ)z + 0 Simplifié : x' = x y' = cos(ϴ)y − sin(ϴ)z z' = sin(ϴ)y + cos(ϴ)z ϴ = Angle en degrés F = cos(ϴ) G = −sin(ϴ) (Note valeur négative) J = sin(ϴ) K = cos(ϴ)	Pivote l'objet de 45 degrés autour de l'axe X : x' = 1x + 0y + 0z + 0 y' = 0x + 0.70711y + −0.70711z + 0 z' = 0x + 0.70711y + 0.70711z + 0
Pivote selon Y	Pivote la géométrie autour de l'axe Y.	x' = cos(ϴ)x + 0y + sin(ϴ)z + 0 y' = 0x + 1y + 0z + 0 z' = −sin(ϴ)x + 0y + cos(ϴ)z + 0 Simplifié : x' = cos(ϴ)x + sin(ϴ)z y' = y z' = -sin(ϴ)x + cos(ϴ)z ϴ = Angle en degrés A = cos(ϴ) C = sin(ϴ) I = −sin(ϴ) (Note valeur négative) K = cos(ϴ)	Pivote l'objet de 45 degrés autour de l'axe Y : x' = 0.70711x + 0y + 0.70711z + 0 y' = 0x + 1y + 0z + 0 z' = -0.70711x + 0y + 0.70711z + 0
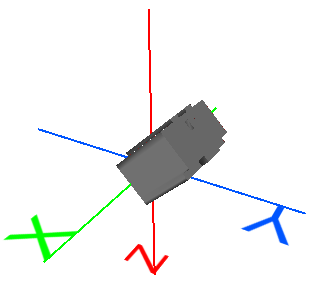
Pivote selon Z	Pivote la géométrie autour de l'axe Z.	x' = cos(ϴ)x + −sin(ϴ)y + 0z + 0 y' = sin(ϴ)x + cos(ϴ)y + 0z + 0 z' = 0x + 0y + 1z + 0 Simplifié : x' = cos(ϴ)x − sin(ϴ)z y' = sin(ϴ)x + cos(ϴ)y z' = z ϴ = Angle en degrés A = cos(ϴ) B = −sin(ϴ) (Note valeur négative) E = sin(ϴ) F = cos(ϴ)	Pivote l'objet de 45 degrés autour de l'axe Z : x' = 0.70711x + −0.70711y + 0z + 0 y' = 0.70711x + 0.70711y + 0z + 0 z' = 0x + 0y + 1z + 0

Notes

Pour effectuer des transformations affines sur place sur des entités géographiques, il faut envisager une reprojection temporaire (Reprojector) dans un système de coordonnées local ou utiliser un CommonLocalReprojector.
Scaler effectue des transformations affines d'échelle en 2D et 3D, avec des options supplémentaires pour des types de géométrie spécifiques et la gestion de l'origine.
Offsetter effectue des traitements affines de translation en 2D et 3D, avec des options d'espace de coordonnées supplémentaires (coordonnées polaires et sphériques, en plus des coordonnées cartésiennes).
Rotator et 3DRotator effectuent des transformations affines de rotation, avec une interface simplifiée pour la valeur de rotation, l'origine (2D) et le choix de l'axe (3D).

Configuration

Ports d'entrée

Ports de sortie

Paramètres

Éditer les paramètres des Transformers

Les paramètres du Transformer peuvent être définis en saisissant directement des valeurs, en utilisant des expressions ou en faisant référence à d'autres éléments de l'espace de travail tels que des valeurs d'attributs ou des paramètres utilisateur. Divers éditeurs et menus contextuels sont disponibles pour vous aider. Pour voir ce qui est disponible, cliquez sur à côté du paramètre concerné.

Définir des valeurs de paramètres

Définir les valeurs

Il existe plusieurs façons de définir une valeur à utiliser dans un Transformer. La plus simple consiste à saisir simplement une valeur ou une chaîne de caractères, qui peut inclure des fonctions de différents types telles que des références d'attributs, des fonctions mathématiques et de chaînes de caractères, et des paramètres traitement.

Utilisation de l'éditeur de texte

L'éditeur de texte fournit un moyen efficace de construire des chaînes de textes (dont les expressions régulières) à partir de données source diverses, telles que des attributs, des paramètres et des constantes, et le résultat est directement utilisé dans le paramètre.

Editeur de texte

Utilisation de l'éditeur arithmétique

L'éditeur arithmétique fournit un moyen simple de construire des expressions mathématiques à partir de plusieurs données source, telles que des attributs et des fonctions, et le résultat est directement utilisé dans un paramètre.

Éditeur arithmétique

Valeur conditionnelle

Définit des valeurs selon un ou plusieurs tests.

Fenêtre de définition de conditions

Contenu

Les expressions et chaînes de caractères peuvent inclure des fonctions, caractères, paramètres et plus.

Lors du paramétrage des valeurs - qu'elles soient entrées directement dans un paramètre ou construites en utilisant l'un des éditeurs - les chaînes de caractères et les expressions contenant des fonctions Chaîne de caractères, Math, Date et heure ou Entité FME auront ces fonctions évaluées. Par conséquent, les noms de ces fonctions (sous la forme @<nom_de_fonction>) ne doivent pas être utilisés comme valeurs littérales de chaîne de caractères.

Types de contenu

Fonctions chaînes de caractères	Ces fonctions manipulent les chaînes de caractères.
Caractères spéciaux	Un ensemble de caractères de contrôle est disponible dans l'éditeur de texte.
Fonctions mathématiques	Plusieurs fonctions sont disponibles dans les deux éditeurs.
Fonctions Date/heure	Les fonctions de dates et heures sont disponibles dans l'Editeur texte.
Opérateurs mathématiques	Ces opérateur sont disponibles dans l'éditeur arithmétique.
Fonctions d'entités	Elles retournent des valeurs spécifiques aux entités.
Paramètres FME	Les paramètres FME et spécifiques au traitement peuvent être utilisés.
Créer et modifier un paramètre publié	Créer ses propres paramètres éditables.

Options - Tables

Outils de tableau

Les Transformers avec des paramètres de style table possèdent des outils additionnels pour remplir et manipuler des valeurs.

Réordonner

Activé une fois que vous avez cliqué sur un élément de ligne. Les choix comprennent :

Ajouter une ligne
Supprimer une ligne
Déplacer la ligne en cours au dessus
Déplacer la ligne en cours en dessous
Déplacer la ligne en cours en haut de liste
Déplacer la ligne en cours en bas de liste

Couper, Copier et Coller

Activé une fois que vous avez cliqué sur un élément de ligne. Les choix comprennent :

Couper une ligne - supprime et copie dans le presse-papiers.
Copie une ligne dans le presse-papiers.
Colle une ligne depuis le presse-papiers.

Copier, copier et coller peuvent être utilisés au sein d'un Transformer ou entre Transfromers.

Filtre

Commencez à taper une chaîne de caractères, et la matrice n'affichera que les lignes correspondant à ces caractères. Recherche dans toutes les colonnes. Cela n'affecte que l'affichage des attributs dans le Transformer - cela ne change pas les attributs qui sont sortis.

Importer

Le bouton d'import remplit la table avec un jeu de nouveaux attributs lus depuis un jeu de données. L'application spécifique varie selon les Transformers.

Réinitialiser/Rafraîchir

Réinitialise la table à son état initial, et peut fournir des options additionnelles pour supprimer des entrées invalides. Le comportement varie d'un Transformer à l'autre.

Note : Tous les outils ne sont pas disponibles dans tous les Transformers.

Pour plus d'information, consulter la section Options des Transformers.

Références

Comportement	Basé sur des entités
Stockage des entités	Non
Dépendances	Aucun
Alias
Historique

FME Community

FME Community dispose d'une mine de connaissances sur FME, avec plus de 20 000 membres actifs dans le monde entier. Obtenez de l'aide sur FME, partagez vos connaissances et entrez en contact avec des utilisateurs du monde entier.

Voir tous les résultats à propos de ce Transformer sur FME Community.

Examples may contain information licensed under the Open Government Licence – Vancouver, Open Government Licence - British Columbia, and/or Open Government Licence – Canada.

3D building model by Berlin Partner für Wirtschaft und Technologie GmbH.